PageRank in SQL

03 December 2013

One of the most profound ideas in the last 20 years is PageRank, the original algorithm of Google’s search engine.

PageRank starts with a simple and clever idea: the importance of a page is determined by how many pages link to it, and how important they are. It’s a link-analysis algorithm, and it ranks pages by how important they are to the entire collection.

In other words, when a source page (like this blog) links to another, target page (like a Wikipedia article), some of the source’s importance should transfer over to the target.

The only things you need are pages and their links. It’s a graph structure.

SQL and Graphs

A graph can be stored in SQL using 2 tables, Nodes and Edges

CREATE TABLE Nodes
(NodeId int not null
,NodeWeight decimal(10,5) not null
,NodeCount int not null default(0)
,HasConverged bit not null default(0)
,constraint NodesPK primary key clustered (NodeId)
)

CREATE TABLE Edges
(SourceNodeId int not null
,TargetNodeId int not null
,constraint EdgesPK primary key clustered (SourceNodeId, TargetNodeId)
,constraint EdgeChk check SourceNodeId <> TargetNodeId --ignore self references
)

Imagine a node is an object like a web page. An edge is a pointer from a source node to a target node, like a hyperlink pointing from one web page to another.

We are preventing a few things. We ignore edges where a node points back to itself. And a node is allowed to point to another node only once.

Imagine a Tiny Web

Imagine the Internet has just 4 web pages: pages 1, 2, 3 and 4. These pages have links between them:

We can store this in SQL

INSERT INTO Nodes (NodeId, NodeWeight)
VALUES
 (1, 0.25)
,(2, 0.25)
,(3, 0.25)
,(4, 0.25)

INSERT INTO Edges (SourceNodeId, TargetNodeId)
VALUES
 (2, 1) --page 2 links to pages 1 and 3
,(2, 3)
,(3, 1) --page 3 links to page 1
,(4, 1) -- page 4 links to the 3 other pages
,(4, 2)
,(4, 3)

Initially, we give all nodes the same weight, 0.25. All nodes start out equal.

Get Ready!

We need to know how many edges each node has pointing away from it. Imagine counting the number of links a web page has going somewhere else. Let’s calculate that and store it in our Nodes table.

declare @TotalNodeCount int

set @TotalNodeCount = (select count(*) from Nodes)

UPDATE n
  --if a node has 0 edges going away then assign it the total # of nodes.
SET n.NodeCount = isnull(x.TargetNodeCount, @TotalNodeCount) 
FROM Nodes n
LEFT OUTER JOIN
(
	SELECT SourceNodeID,
		TargetNodeCount = count(*)
	FROM Edges
	GROUP BY SourceNodeId
) as x
ON x.SourceNodeID = n.NodeId

Get Set!

Let’s look at the most important part: calculating how we transfer weight from source nodes to targets.

SELECT
	 e.TargetNodeId
	,TransferWeight = sum(n.NodeWeight / n.NodeCount) * @DampingFactor
FROM Nodes n
INNER JOIN Edges e
  ON n.NodeId = e.SourceNodeId
GROUP BY e.TargetNodeId

You can see there’s a damping factor, which is the percentage of a node’s weight that gets transferred via its edge to another node.

We also include a margin of error, which is a small number that represents an acceptable amount of precision.

Now we’re ready to run PageRank.

GO!

declare @DampingFactor decimal(3,2) = 0.85 --set the damping factor
	,@MarginOfError decimal(10,5) = 0.001 --set the stable weight
	,@TotalNodeCount int
	,@IterationCount int = 1

-- we need to know the total number of nodes in the system
set @TotalNodeCount = (select count(*) from Nodes)

-- iterate!
WHILE EXISTS
(
	-- stop as soon as all nodes have converged
	SELECT *
	FROM dbo.Nodes
	WHERE HasConverged = 0
)
BEGIN

	UPDATE n SET 
	NodeWeight = 1.0 - @DampingFactor + isnull(x.TransferWeight, 0.0)

	-- a node has converged when its existing weight is the same as the weight it would be given
	-- (plus or minus the stable weight margin of error)
	,HasConverged = case when abs(n.NodeWeight - (1.0 - @DampingFactor + isnull(x.TransferWeight, 0.0))) < @MarginOfError then 1 else 0 end
	FROM Nodes n
	LEFT OUTER JOIN
	(
		-- Here's the weight calculation in place
		SELECT
			e.TargetNodeId
			,TransferWeight = sum(n.NodeWeight / n.NodeCount) * @DampingFactor
		FROM Nodes n
		INNER JOIN Edges e
		  ON n.NodeId = e.SourceNodeId
		GROUP BY e.TargetNodeId
	) as x
	ON x.TargetNodeId = n.NodeId

	-- for demonstration purposes, return the value of the nodes after each iteration
	SELECT
		@IterationCount as IterationCount
		,*
	FROM Nodes

	set @IterationCount += 1
END

Victory!

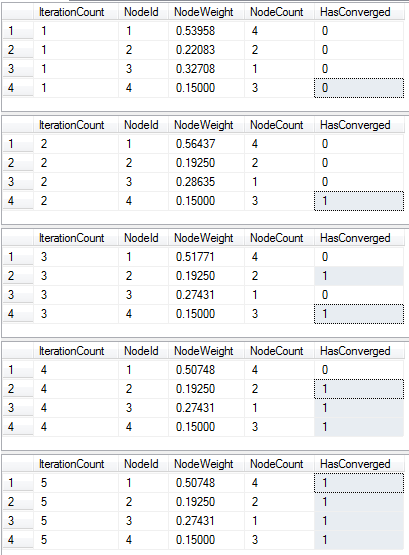
This example takes 5 iterations to complete. It turns out computing PageRank for the entire world wide web takes only 100 iterations.

I’d recommend you try this out yourself. My code is available on GitHub.

Happy Coding!